Multiple constraints in STV elections: OpenTally dev log
OpenTally is open source software currently under development for the counting of elections using STV and related systems. Part of its feature set is the implementation of constraints on elections: for example, where a certain minimum or maximum number of candidates must be elected from a particular group.
In OpenTally, and its predecessor pyRCV2, implement the Gray–Fitzgerald [1] method of constraints on STV elections: each time a candidate is declared elected or excluded, any candidate who must be elected to secure a conformant result is declared guarded, and any candidate who must not be elected is declared doomed. Doomed candidates are immediately excluded, and guarded candidates are protected from exclusion.
The application of this method is straightforward in the case of one constraint. Once the number of non-excluded constrained candidates equals the specified minimum, all such candidates must be guarded; once the number of elected constrained candidates equals the specified maximum, all corresponding hopeful candidates must be doomed.
The situation with more than one constraint is more complicated. The general approach is set out by Hill in [2], but is computationally difficult when there are a large number of candidates and constraints. In [3], Otten presents an alternative method which yields the same results but scales more efficiently. Otten presents the method for the case of 2 independent constraints, and remarks that ‘the same logic can be applied with higher dimensions if required’. The extension of the method to higher dimensions, however, is not necessarily completely clear from the 2D case alone.
To see how Otten's method can be extended to more than 2 independent constraints, let us first consider the 1-dimensional case, i.e. with a single constraint. Suppose the candidates are divided into 3 disjoint categories (1, 2 and 3), and a certain minimum and maximum must be elected from each. Otten's grid would look as follows:

The blue cells indicate where the minimums/maximums would initially be set from the constraints. The asterisk (wildcard) indicates a total across a particular constraint – in this case, as there is only 1 constraint, there is a single grand total cell.
Consider now the addition of a second constraint with 2 disjoint categories (A and B). The grid must be extended by taking the single row and duplicating it vertically, such that there is additionally a row for A and a row for B:
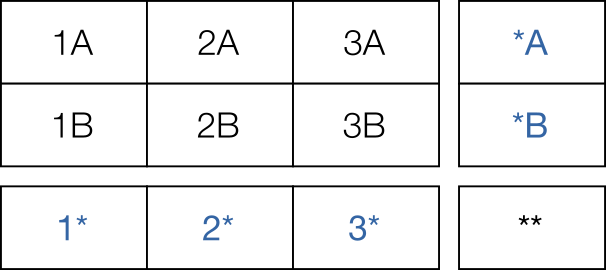
This replicates the grid shown in Otten's paper. As before, the blue cells indicate where the minimums/maximums would initially be set from the constraints – i.e. the minimums/maximums for each disjoint category within each constraint, disregarding any combinations of constraints.
Consider now the addition of a third constraint with 2 disjoint categories (X and Y). The grid must be extended by taking the single plane and duplicating it in the third dimension, such that there is additionally a plane for X and a plane for Y:

Again, the blue cells indicate where the minimums/maximums would initially be set. The other totals/subtotals cells are shown in bold type.
In this image, the structure of the n-dimensional grid becomes more apparent. In any number of dimensions, the blue cells, where the maximums/minimums are initially set from the constraints, are the cells with exactly 1 non-wildcard index. The cells with no wildcard indexes represent candidates in each concrete combination of constraint categories. The remaining cells with >1 non-wildcard indexes form totals and subtotals across various different constraints.
We can see now how to extend Otten's methodology to higher dimensions. Consider rule 4 of Otten's method: ‘The row/column minimum must be at least the sum of the minima of the items in the row/column’. We can extend this in the ≥3D case beyond only rows/columns to include all totals/subtotals cells.
We must begin with the cells with 1 wildcard index, and sum across the wildcard axis – for example, in 2A* the minimum must be at least the sum of the minima in 2AX and 2AY. Once all cells with 1 wildcard index have been processed, we then turn to cells with 2 wildcard indexes – for example, in *A* the minimum must be at least the sum of the minima in 1A*, 2A* and 3A* (which would have been calculated above), and that in *AX and *AY. We continue, processing cells with increasing numbers of wildcard indexes, until finally processing the grand total cell (all wildcards).
This forms the basis for the handling of multiple constraints in OpenTally.
References
[1] Gray AJ, Fitzgerald J. Regulations applying the principle of proportional representation by the method of the single transferable vote illustrated by an example. London: Proportional Representation Society; 1955.
[2] Hill ID. STV with constraints. Voting Matters. 1998 May; (9): 2–3. http://www.votingmatters.org.uk/ISSUE9/P1.HTM
[3] Otten J. STV with multiple constraints. Voting Matters. 2001 Apr; (13): 4–7. http://www.votingmatters.org.uk/ISSUE13/P3.HTM