Reverse engineering software licensing from early-2000s abandonware – Part 1

Background

This series concerns a software licensing system used in a proprietary software application from circa 2004. The software was available in an unregistered trial mode with limited functionality. A free licence could be obtained by registering online with the software vendor. The software became abandonware circa 2009 when it ceased to be offered, and while the software binary has been archived, to date there has been no effort to restore the functionality once available with a free licence.

Disassembling the binary

In an earlier post about another reverse engineering project, I used IDA Free as a disassembler. Since then, the US National Security Agency has released its reverse engineering tool, Ghidra, as open source software, which I will use for this project.

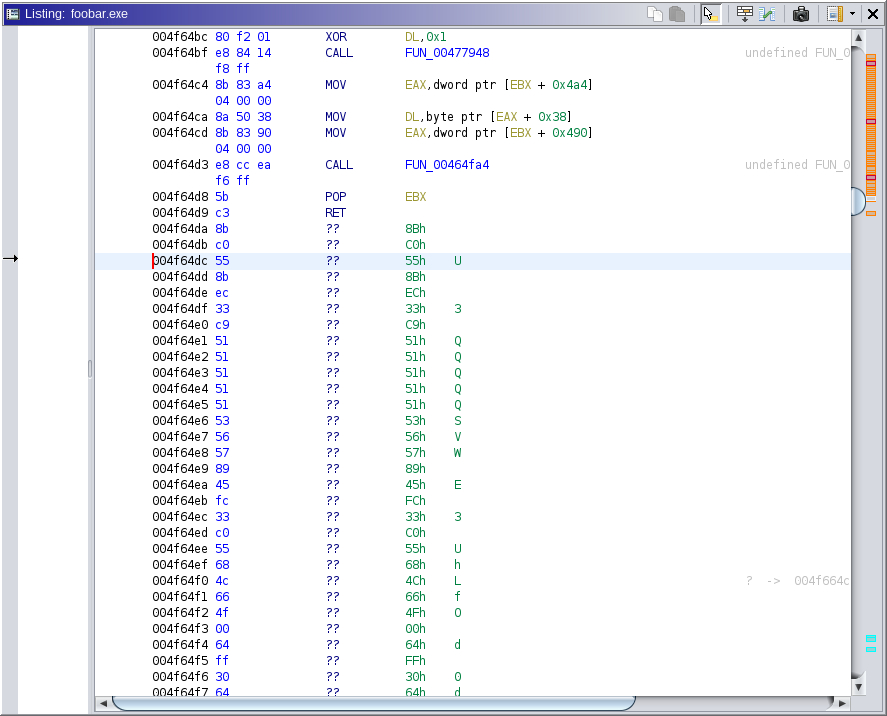
In comparison to IDA, Ghidra requires some coaxing to correctly disassemble the software binary. For example, see the following Ghidra disassembly:

IDA automatically identifies a function at 0x4f64dc, but this is not identified by Ghidra. As it turns out, this is one function which will be relevant to our analysis. Ghidra can perform a more extensive analysis via Analysis → One Shot → Aggressive Instruction Finder, but the result is still incomplete.

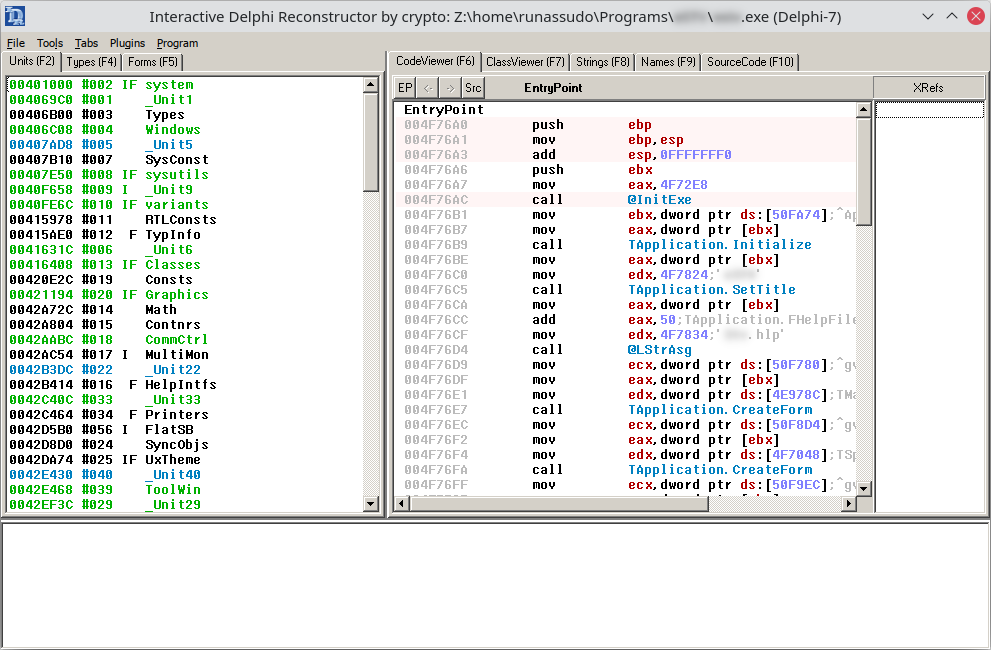
We know from the metadata of the software binary that this build was produced in Delphi 7 (released 2002). Both Ghidra and IDA have trouble with Delphi binaries, resulting in missing symbol names and missing labels relating to Delphi classes. To overcome this, we leverage IDR, the Interactive Delphi Reconstructor, which extracts the relevant symbols from the binary:

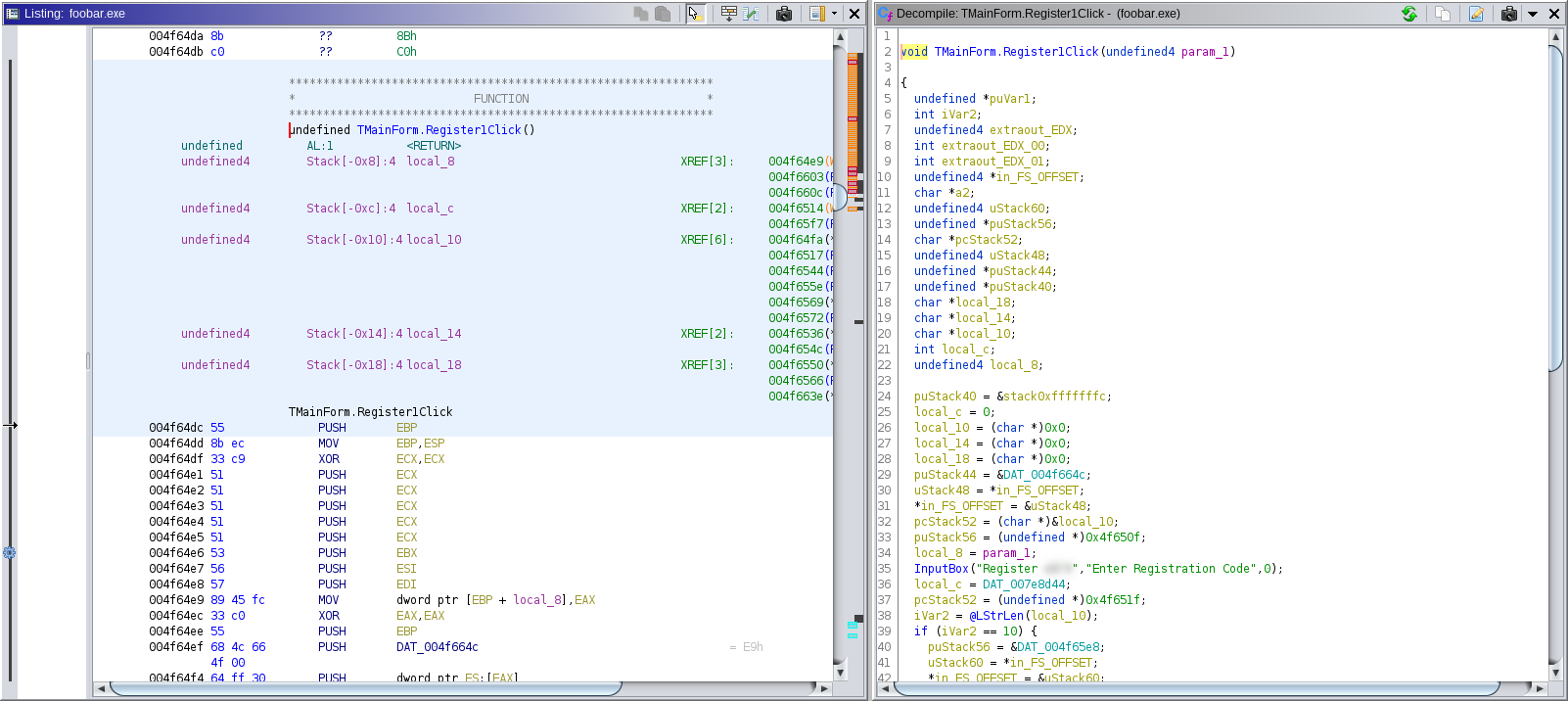
We can then import this data into Ghidra using Dhrake, which identifies the function at 0x4f64dc as TMainForm.Register1Click, and also identifies other functions such as InputBox and @LStrLen, which will greatly help with analysing the disassembly:

Bypassing the registration code check

We note that TMainForm.Register1Click contains references to "Enter Registration Code" and related strings which appear in the dialog when the user accesses the registration feature of the software.¹ It appears, then, that this is a relevant target for our analysis, so we examine in greater detail Ghidra's decompiled output, which is a feature not available in IDA Free. The relevant code reads:

void TMainForm.Register1Click(undefined4 param_1) {
  // ...
  local_c = DAT_007e8d44;
  // ...
  if (...) {
    // ...
    if (...) {
      DAT_007e8d44 = 1;
    }
    // ...
    if (...) {
      DAT_007e8d44 = 2;
    }
    // ...
  }
  if (DAT_007e8d44 != local_c) {
    pcStack52 = "Registration code accepted";
    puStack56 = (undefined *)0x0;
    uStack60 = local_8;
    FUN_004f5694();
    // ...
  }
  // ...
}

We observe that, in the above decompiled code, the value of DAT_007e8d44 is stored in local_c. Under certain conditions, DAT_007e8d44 is then set to 1 or 2, and this is compared with the original value of DAT_007e8d44. If the values differ, there is a reference to the promising-looking string "Registration code accepted". Presumably, the default value of DAT_007e8d44 is 0.

We therefore hypothesise that DAT_007e8d44 contains a flag representing whether the software is registered. During the registration function, if the provided registration code is valid, DAT_007e8d44 is set to 1 or 2, which results in the "Registration code accepted" branch being taken. To test this hypothesis, we turn to our debugger.

In this project, I am running the software on Linux using Wine, which comes with its own debugger, winedbg, which has GDB integration. Since mid-2021, Ghidra has debugger support, but it does not play well with winedbg or Wine under GDB, so we will use winedbg/GDB manually.

In the below screenshot, we can see that 0x4f65f2 is the address where DAT_007e8d44 is read, corresponding to the if (DAT_007e8d44 != local_c) check:

Using winedbg/GDB, we therefore set a breakpoint at 0x4f65f2 before allowing the software to run:

$ winedbg --gdb foobar.exe
Wine-gdb> b *0x4f65f2
Breakpoint 1 at 0x4f65f2
Wine-gdb> c
Continuing.

We then enter the registration form, input an arbitrary registration code, and wait for the breakpoint to be triggered. When this happens, we confirm that the default value of DAT_007e8d44 is, as we suspected, 0:

Breakpoint 1, 0x004f65f2 in ?? ()
Wine-gdb> x/wx 0x7e8d44
0x7e8d44:       0x00000000

We then manually change the value at address 0x7e8d44 to equal 1, and resume execution:

Wine-gdb> set *0x7e8d44=1
Wine-gdb> c
Continuing.

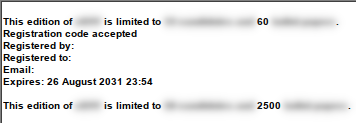
We are greeted by a pleasing message which probably no one has seen in over a decade:

(The ‘60’ limit is displayed when the program launches. The registration information is displayed and the limit increased to ‘2500’ once the registration function concludes.)

Reverse engineering the registration code validation

Although we have unlocked the functionality of the software, it would be nice if we were able to do this without needing to use memory manipulation each time. Returning to the TMainForm.Register1Click decompilation, we expand our scope slightly:

void TMainForm.Register1Click(undefined4 param_1) {
  // ...
  InputBox("Register FooBar","Enter Registration Code",0);
  local_c = DAT_007e8d44;
  // ...
  iVar2 = @LStrLen(local_10);
  if (iVar2 == 10) {
    // ...
    @LStrCopy(local_10,1,5,&local_14);
    a2 = local_14;
    @LStrCopy(local_10,6,5,&local_18);
    @LStrCat3(&local_10,local_18,a2);
    DAT_007e8d64 = StrToInt64(local_10);
    DAT_007e8d68 = extraout_EDX;
    iVar2 = @_llmod(DAT_007e8d64,extraout_EDX);
    if ((extraout_EDX_00 == 0) && (iVar2 == 1)) {
      DAT_007e8d44 = 1;
    }
    iVar2 = @_llmod(DAT_007e8d64,DAT_007e8d68);
    if ((extraout_EDX_01 == 0) && (iVar2 == 0x15)) {
      DAT_007e8d44 = 2;
    }
    // ...
  }
  if (DAT_007e8d44 != local_c) {
    pcStack52 = "Registration code accepted";
    // ...
  }
  // ...
}

We see that the InputBox function is called with the title and prompt of the registration code input window. The user's input is presumably stored in local_10, we then call @LStrLen, and proceed to manipulate the registration code further only if the length is 10. Valid registration codes, then, must be 10 characters long.

There are then calls to @LStrCopy(local_10,1,5,&local_14); and @LStrCopy(local_10,6,5,&local_18);. @LStrCopy is an internal Delphi function and is not well documented, but we can surmise that this acts like a substring function, copying the first 5 characters of the registration code to local_14, and the last 5 characters to local_18.

There is then a call, effectively, to @LStrCat3(&local_10,local_18,local_14);. Again, this is an undocumented internal Delphi function, but Google leads us to a random Chinese forum post which lets us know that this performs local_10 := local_18 + local_14. The overall effect, then, is to swap the first and last 5 characters of the registration code.

Then the swapped registration code is passed to StrToInt64, which, as expected given the name, parses a string into a 64-bit integer. But this software binary, from 2004, is a 32-bit application, so how is a 64-bit integer represented here? The Delphi documentation tells us that it is stored as edx:eax.

We can confirm this using the debugger. Using winedbg/GDB, we set a breakpoint just after the StrToInt64 call, and inspect the values of eax and edx after inputting 1234567890 as the registration code:

$ winedbg --gdb foobar.exe
Wine-gdb> b *0x4f6586
Breakpoint 1 at 0x4f6586
Wine-gdb> c
Continuing.

Breakpoint 1, 0x004f6586 in ?? ()
Wine-gdb> info reg
eax            0x94a81b79          -1800922247
ecx            0x0                 0
edx            0x1                 1
ebx            0x1026e58           16936536
[...]

Note that edx concatenated with eax equals 0x194a81b79, which in decimal is 6789012345, as expected.

Returning to TMainForm.Register1Click, we note that this result is stored in DAT_007e8d64 (low 32 bits) and DAT_007e8d68 (high 32 bits). However, the decompilation of the next part of the function is incorrect, so we turn to the raw disassembly, which relevantly reads:

; ...
004f6586 6a 00           PUSH       0x0
004f6588 68 c3 b2        PUSH       0xa1b2c3
         a1 00
004f658d 8b 05 64        MOV        EAX,dword ptr [DAT_007e8d64]
         8d 7e 00
004f6593 8b 15 68        MOV        EDX,dword ptr [DAT_007e8d68]
         8d 7e 00
004f6599 e8 1a f2        CALL       @_llmod
         f0 ff
004f659e 83 fa 00        CMP        EDX,0x0
004f65a1 75 0f           JNZ        LAB_004f65b2
004f65a3 83 f8 01        CMP        EAX,0x1
004f65a6 75 0a           JNZ        LAB_004f65b2
004f65a8 c7 05 44        MOV        dword ptr [DAT_007e8d44],0x1
         8d 7e 00 
         01 00 00 00
                     LAB_004f65b2 
; ...

It looks like we call @_llmod, passing as one parameter the parsed registration code, and passing as the second parameter (on the stack) the Int64 0xa1b2c3.² Presumably, this performs the modulo (remainder after division) operation.

We then check to see if edx = 0 and if eax = 1, and if both are true, we move the value 1 into DAT_007e8d44 (which, as previously discovered, indicates the registration code is valid).

Presumably, then, edx:eax is the Int64 result of the modulo operation, and the code is considered valid if the value of the registration code (the 2 halves having been swapped) modulo 0xa1b2c3 equals 1. A trivial registration code which satisfies this requirement is 0000100000.³

We input this code into the software, and confirm that the code is accepted.

Next steps

In this part, we reverse engineered the registration code verification mechanism, and produced a valid registration code which can be used to unlock the full functionality of the software.

However, this code-based licensing mechanism was not the actual mechanism in use in 2004. In part 2, we investigate this other licensing mechanism.

Footnotes