Later-no-harm and the ‘Wright’ method of single transferable vote

Later-no-harm is a criterion for preferential voting methods which provides that ‘Adding a later preference to a ballot should not harm any candidate already listed’ [1]. The most well-known voting systems which comply with later-no-harm are the single transferable vote (STV), and its single-winner variant, instant runoff voting.

Proponents of STV tend to place great emphasis on later-no-harm. Indeed, it is arguably later-no-harm which distinguishes STV from related systems, such as Condorcet methods. For example, section 10.10 of the 2018 Amherst Home Rule Charter provides that ‘A voting method shall be considered [the single transferable vote] if the voter ranks candidates in order of preference and a voter's lower ranked choice does not impact the likelihood of a higher ranked choice being elected’ (emphasis added).

STV methods tend to guarantee later-no-harm, because further preferences on a ballot are examined only once earlier preferences have been either elected or excluded (and therefore cannot be harmed by the later preference).

The ‘Wright’ method is an exception, which proposes that the count is reset each time a candidate is excluded, yielding a reiterative process. In all iterations but the last, candidates then are not elected but merely ‘provisionally elected’, but later preferences are still examined.

In this article we show by way of example that this causes the ‘Wright’ method to fail later-no-harm.

Example

This is example is adapted from an example by ID Hill [2], modified to apply to the particular specifications of the ‘Wright’ method and weighted inclusive Gregory method.

Consider an election with 8 candidates, A through H, competing for 5 seats. Suppose the votes are:

Votes	Preferences
2500	A > C > D > F
2400	B > C > E
700	D > F
500	E
200	F
600	G
300	H > B > C
7200	Total

Under the ‘Wright’ method, in the 1st iteration A and B are provisionally elected on first preferences. On distributing A's surplus, C is provisionally elected.

On distributing B's surplus, note that the next preference, C has already been provisionally elected. Because the ‘Wright’ method does not transfer votes to already elected candidates, votes are instead transferred to E, who is in turn provisionally elected.

Fewer than 5 candidates have been provisionally elected, so F is to be excluded:

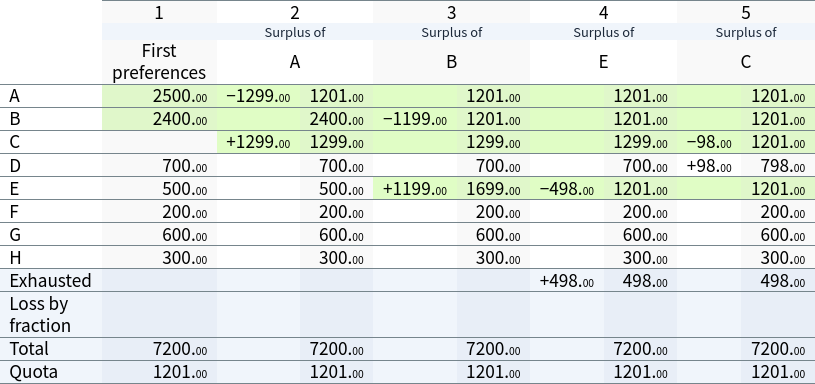
As F is excluded, the ‘Wright’ method requires all candidates to be un-elected, and the process reset from the count of first preferences. Again, A, B, E and C are provisionally elected. Again, fewer than 5 candidates have been provisionally elected, so now H is to be excluded:

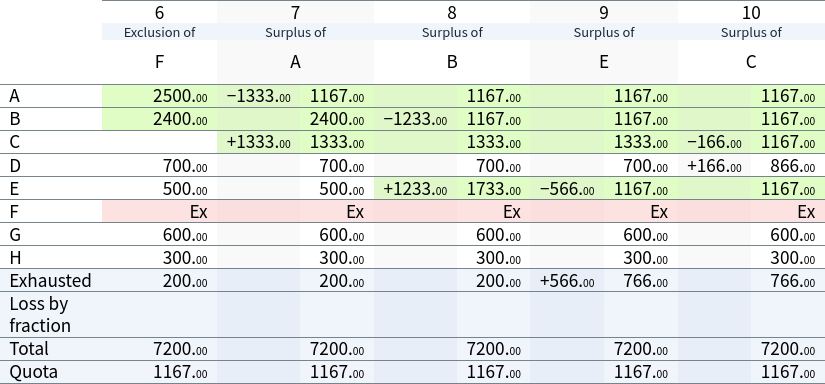
In the final iteration, the provisionally elected candidates are B, A, D, C and E. As 5 candidates have been elected, the count is complete:

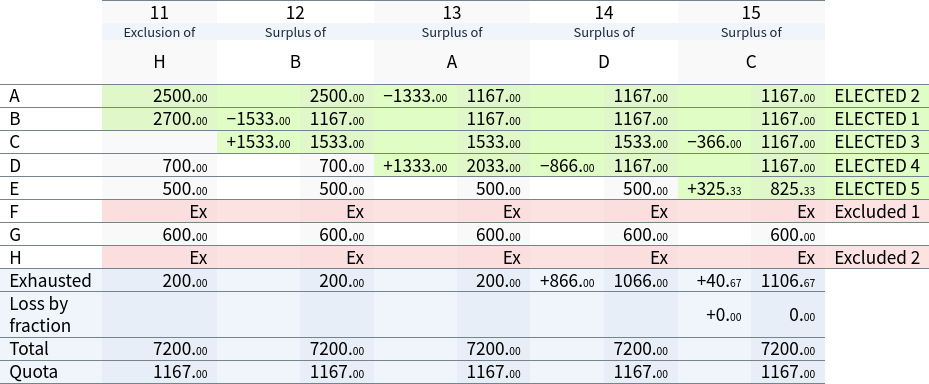
Now consider the same election, but with a slight modification, where the 2400 ‘B > C > E’ voters add F to the end of their preferences:

Votes	Preferences
2500	A > C > D > F
2400	B > C > E > F
700	D > F
500	E
200	F
600	G
300	H > B > C
7200	Total

Note that, in the original election, candidates B, C and E were all elected. Later-no-harm requires that adding F to the end of the preferences should not harm any of B, C or E. Let us see if this holds true under the ‘Wright’ method.

In the 1st iteration, as before, A and B are provisionally elected on first preferences. After the distribution of their surpluses, E and C are provisionally elected. In this case, surplus votes are now transferred from E to F. Whereas F was previously the first-excluded candidate, F is now saved from exclusion, and H is instead to be excluded:

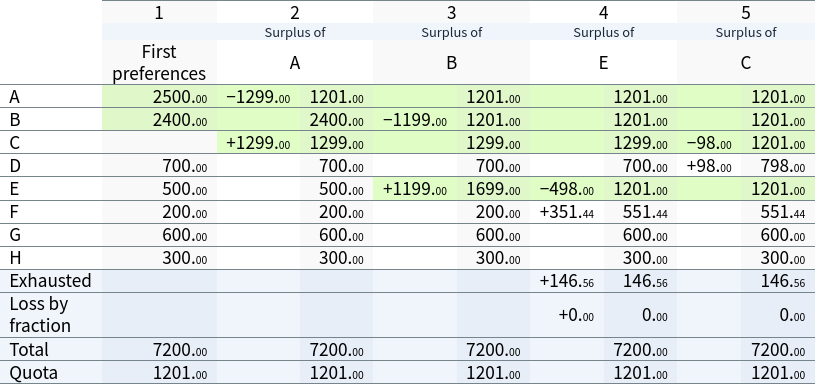
In the 2nd iteration, H's exclusion causes B's surplus to be distributed before A's. Because, in this situation, C has not yet been provisionally elected, B's surplus votes are transferred to C, not E.

When C's surplus is eventually distributed, the votes are reweighted such that insufficient votes are transferred to E to secure their election. Rather, G is now to be excluded:

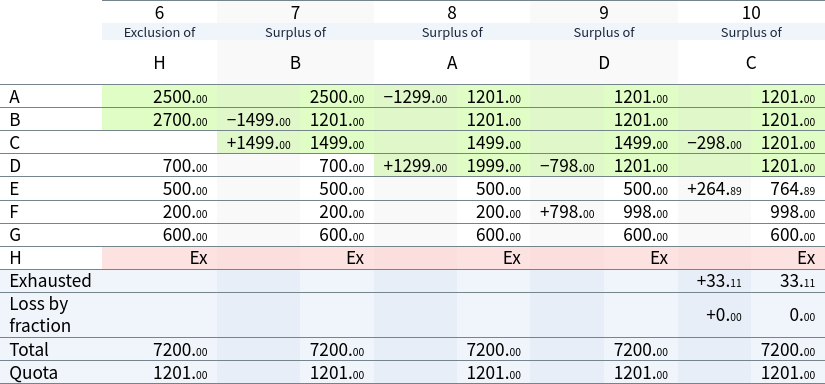
G's exclusion does not improve the situation for E. Rather, because it is now A's first preference votes which ‘skip over’ candidate C, surplus distributions at a comparatively greater value enable candidate F to eventually reach the quota and become the final elected candidate:

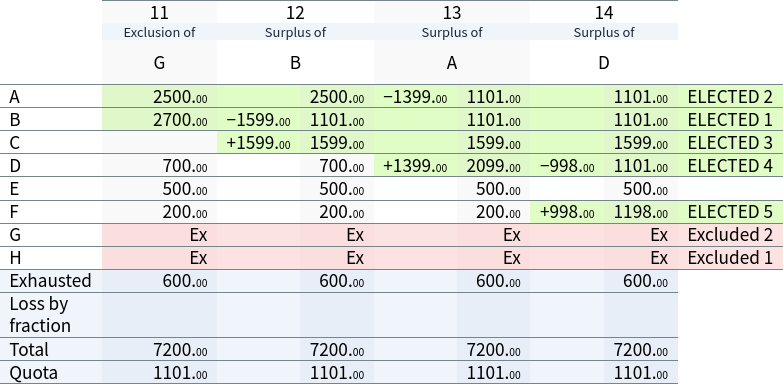
By adding additional preferences at the end of their ballot, ‘B > C > E’ voters harmed one of their more preferred candidates, E, who is elected if the additional preference is omitted, but who is not elected if the additional preference is listed. This is a violation of later-no-harm.

Summary

The ‘Wright’ method violates later-no-harm because it enables later preferences to be considered when a more-preferred candidate is ‘provisionally’ (but not finally) elected. Perversely, examining later preferences beyond a ‘provisionally elected’ candidate can result in that candidate failing to be elected in a later round.

Specifically, as noted by Hill [2], this issue arises because the ‘Wright’ method does not transfer votes to previously elected candidates during a surplus distribution. Therefore, while the result is independent of the order of exclusion, it is dependent on the order of provisional election.

To address this fault requires enabling transfers to be made to previously elected candidates, using the Meek method. All ballot papers can therefore be treated equally, and the result is independent both of the order of exclusion and the order of election. The Meek method also obviates the need for a ‘provisional election’ mechanism, and as with other STV systems, later preferences are examined only when a candidate is definitively elected or excluded, ensuring that later-no-harm is observed. In the Meek method, A, B, C, D and E are the elected candidates in either situation.

References

[1] Woodall DR. Properties of preferential election rules. Voting Matters. 1994; 1(3): 8–15. https://www.votingmatters.org.uk/ISSUE3/P5.HTM

[2] Hill ID. Comments on Newland's paper. Voting Matters. 2007; (23): 1–2. https://www.votingmatters.org.uk/ISSUE23/I23P1.pdf